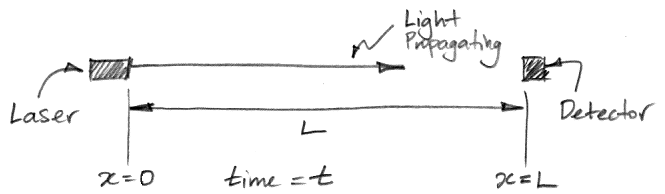
Figure: Apparatus for Measuring the Speed of Light.
[23-MAR-24] Here we derive the Lorentz Transform, which is the mathematical expression of Special Relativity. The Lorentz Transform allows us to calculate how much shorter a moving ruler will appear to us as it moves by, how much slower a moving clock will run compared to a stationary clock, and how much longer an unstable sub-atomic particle will last if it is moving close to the speed of light. There are the phenomena of length contraction and time dilation. Our derivation will require only simple algebra to complete. We continue our investigation of fast-moving objects in Relativistic Collisions.
We have the following apparatus for measuring the speed of light. It contains a clock that measures time, t, and a ruler that measures position, x. A laser at position x = 0 m turns on at time t = 0 s. Its light propagates towards a target at position x = L. The light arrives at the detector at time t = a. The speed of light is c = L/a.

We set up the apparatus in our laboratory on the surface of the Earth. We point the laser in the direction of the Earth's 30 km/s orbital velocity. We measure c = 299,792 km/s. We rotate the apparatus and point the laser in the opposite direction. Some of us are expecting to get an answer 60 km/s higher this time, because the Earth is carrying the target towards the advancing light, while it carried the target away from the advancing light in the first measurement. But we measure c = 299,792 km/s again. We repeat our measurement in many orientations and we always get the same answer. We repeat our measurement in the same orientation a hundred times throughout the day, and we always get the same answer.
What we have described is a simplified version of the series of experiments performed by Michelson and Morley in 1887, and repeated in a variety of ways in the decades that followed. The speed of light is the same for all observers moving at constant velocity, regardless of how fast they move, the direction of the light, or which observer holds the source of the light.
In the following sections, we will determine how it is possible for different observers moving at different velocities to measure the same beam of light to be moving at the same speed. For brevity and clarity, but without loss of generality, we will conduct our investigation in one spatial dimension. We will arrive at the one-dimensional Lorentz Transformation, which is easily extended to three dimensions.
For our purposes, an inertial frame is a ruler that is not accelerating, accompanied by a set of synchronized clocks. The ruler measures position, x, along a line. In one direction, x increases and in the other it decreases. Along the ruler we have the clocks. Observers who are stationary with respect to the ruler agree that the clocks read exactly the same time. We say the clocks are synchronized within the frame of reference. We can check the synchronisation of the clocks at any time with a machine that travels along our ruler at a constant velocity u. We release this machine from x = 0 m at time t = b s. When it passes a clock at position x = L, the clock should read b + L/u. If the clock is wrong, we correct it.
The following diagram shows two frames of reference, F and F |. We could place them right on top of one another, so that their rulers were along the same line, but this would be hard to draw. Let us imagine that their rulers are parallel and close together. The frames are moving with respect to one another. So far as frame F is concerned, frame F | is moving at velocity v, where v is positive. Conversely, so far as frame F | is concerned, frame F is moving at −v.
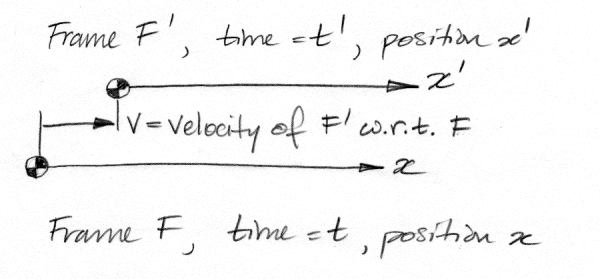
Suppose something happens in the space between the two rulers, so that observers on both rulers have a clear view of the event. This event could be a beam of light being emitted by a laser or a beam of light striking a target. When this event occurs, it does so at a position x in F and x | in F |. We make sure there is a clock right there on both rulers. The clock in F is synchronized with all other clocks in F and reads time t, while the clock in F | is synchronized with all other clocks in F | and reads time t |.
The values of t and t | could be different because one clock is far behind the other. But let us suppose, without loss of generality, that at t = 0 s and x = 0 m in F corresponds to t | = 0 s and x | = 0 in F |. At time zero in both frames, the zero-positions on the rulers of both frames are next to one another.
We are inclined to assume that the clocks facing one another across the small space between the rulers will always read the same time. And we are inclined to assume that the 1-mm divisions on the two rulers will have the same length. But we will make neither assumption. We will assume only that one frame is moving at v with respect to the other and the speed of light will be c in both frames. These two observations are so constraining that they already dictate what we will see on either side of the small gap between the rulers, so we cannot make any further assumptions. All we can do is figure out the consequences of the assumptions we have already made.
The principle of relativity states that a distance or a length of time we measure will not depend upon where we place the point x = 0 m, nor the moment we choose to call t = 0 s, nor will it matter which of two frames we choose to call F or F |. We might protest that F | moves in F at v while F moves in F | at −v. But we could just as easily construct F | with x | pointing in the opposite direction, in which case each frame would be moving in the other at v, so this difference in sign cannot not break the physical symmetry between the two frames, nor cause a violation of the principle of relativity.
Consider an event that occurs at position x and time t in frame F. In frame F | the same event has position x | and time t |. Because x and t correspond uniquely to x | and t |, there exist two mathematical equations that allow us to calculate x | and t | from the values of x and t. Together, these two equations constitute the transformation function from F to F |. Our task is to determine these equations. Our first step is to argue that the transformation has the following form, where p, q, r, and s are numbers.
Suppose we keep t constant. The slope of a graph of x | versus x will be a straight line with slope p. The graphs of x | versus t for constant x, and of t | versus x for constant t, and of t | versus t for constant x, will also be straight lines. We say the transformation function is linear in x and t.
Suppose the transformation function were not linear. Suppose the slope of the graph of x | versus x for fixed t were a curved line. Without loss of generality, suppose the slope of the graph is 1.0 at x = 0 m and 2.0 at x = 1000 m. Observer A stands in F at x = 0 m and looks at the ruler in F | that moves by at velocity v. She observes that the 1-mm divisions on the moving ruler are the same length as the 1-mm divisions on her own ruler. Observer B stands in F at x = 1000 m. He looks across at the moving ruler and observes that its 1-mm divisions are half as long as the 1-mm divisions on his own ruler. Now suppose we press a button and all the distance marks on the ruler in F drop by 1000 m. Observer B is now at position x = 0 m. Our non-linear transformation tells us that B will now observe that the 1-mm markings on the moving ruler are the same size as the 1-mm markings on his own ruler. We have arrived at a contradiction: it is impossible for our choice of where to place x = 0 m on our own ruler to have any effect upon the apparent size of the 1-mm divisions of the ruler in F |.
We can use the same argument for any curvature in the graph of x | versus x for constant t, however slight. No such curvature is possible. The graph must be straight. Our argument is an application of the principle of relativity: the location of x = 0 m and the moment of t = 0 s cannot change our observations of length or duration. There is nothing impossible about the ruler appearing to shrink from the point of view of observers on F, but it is impossible for the ruler to appear to shrink by different amounts at different places or times in F. By the same argument, we can show that the graph of x | versus t for constant x must be straight, as well as the graph of t | versus x for constant t, and the graph of t | versus t for constant x.
The transformation function is linear. Our job is to deduce the constants p, q, r, and s using the following constraints: the transform will obey the principle of relativity, the transform will predict that light will travel at speed c in both frames, and the transform will agree that one frame is moving at velocity v with respect to the other.
The point x | = 0 m moves with velocity v with respect to F. Without loss of generality, we assumed the points x | = 0 and x = 0 m were coincident at time t = 0 s in F and t | = 0 s in F |. These two constraints permit us to derive a relation between the constants p and q in our transformation function.
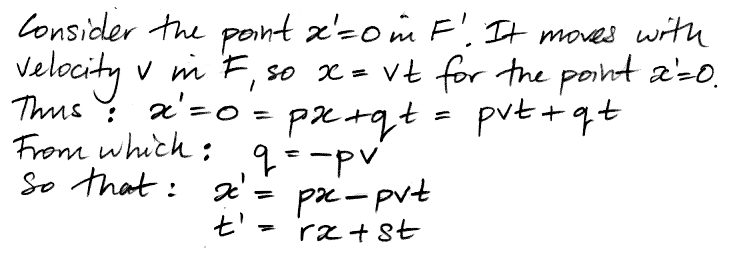
We are sitting on a train looking outside. We are F | and the world outside is F. Houses appear to have the same dimensions they would if we were standing on the ground, but they are moving past us. For all practical purposes, we have p = 1 so that x | = x − vt. At t = 0 s the two rulers are lined up and their divisions are the same length. When v << c, we expect p = 1. By the same argument, s = 1 and r = 0 s/m for v << c, so that we will obtain the familiar relation t | = t. Only when v becomes significant with respect to the speed of light will we see p ≠ 1, s ≠ 1, and r ≠ 0.
Observers in both F and F | will measure the speed of a beam of light to be c. If the light propagates in the positive direction, both observers will measure it to be moving at velocity c. Suppose a beam of light leaves the point x = 0 m at time t = 0 m. At time t, an observer in F will find the beam has propagated to x = ct. At time t |, an observer in F | will find the beam has propagated to x | = ct |. The same is true for a beam of light propagating in the negative direction. Observers in F and F | will measure the beam's velocity to be −c. These two considerations, of light going in both directions, allow us to express both r and s in terms of p.

At time t = 0 s, t | = −pvx/c2. For x > 0 m in F at time t = 0 s, the clocks on F | lag behind the clocks on F. The farther we go from x = 0 m, the greater the lag becomes. In the negative direction, the opposite is true: the clocks on F | are increasingly ahead of the clocks on F. Suppose two events occur simultaneously in F at time t = 0 s, but one event occurs at x = 0 m and the other occurs at x > 0 m. An observer in F |, however, will claim that the event at x > 0 m occurred before the event at x = 0 m. Events in different locations that are simultaneous in F will not be simultaneous in F |. Our transformation function preserves the speed of light, but it does not preserve simultaneity.
Consider the segment of the ruler in F that extends from x = 0 m to x = L. At time t = 0 s our transformation function tells us that one end of this segment is at x | = 0 m and the other is at x | = pL. For v << c we have p ≈ 1, but for larger v we expect p ≠ 1. We don't yet know if p < 1 or p > 1, but let us suppose p > 1. To the observer in F, the ruler in F | appears to have contracted by a factor of p.
When we measure the length of a moving object, we mark the position of its front end and its back end on our ruler. We must make these marks simultaneously, or else the object will move between the time we make the first mark and the time we make the second mark. But simultaneity is not conserved between frames. If simultaneity is not conserved, nor will length be conserved.
If the ruler in F | appears contracted by a factor of p for an observer in F, how does the ruler in F appear to an observer in F |? The principle of relativity dictates that the ruler in F will also appear to be contracted. If x = L and t = 0 s corresponds to x | = pL, then x | = L and t | = 0 s will correspond to x = pL. This length constraint permits us to determine p in terms of v and c.

The constant p is the Lorentz Factor, denoted γ, and often called gamma. When v << c, γ ≈ 1. When v is larger, γ > 1. For example, when v = c/2, γ = 1.15.
The transformation function from F to F | is below. Its constants are a function of v and c only. It conserves the speed of light and is symmetric in its contraction of length and time.
The transformation function from F | to F must have the same form as above. The principle of relativity dictates that what is true for one frame looking at a second fram must be true looking from the second to the first. Here is the inverse transform, which converts x | and t | into x and t.
The only difference between the original transform and its inverse is that the terms in v have changed sign. The sign change is a consequence of the fact that F moves at −v in F |, while F | moves at v in V. If we defined x | in the opposite direction, the transform and its inverse would be exactly the same.
Suppose v = c/2. We have γ = 1.15. In F, at t = 0 s we note the value of x | that coincides with x = 0 m and x = L. Let L = c × 0.5 s = 150×103 km = 150 Mm. We observe x | = 0 m at x = 0 m and x | = γL = γc/2 = 172 Mm at x = L = 150 Mm. A distance 172 Mm in F | extends only 150 Mm in F. In general, distances in F | are shrunk in the direction of v by a factor of γ when viewed from F.
The observer in F |, however, sees us marking the position of x | = γL at time t | = −γvL/c2 = −γ/4 = −0.29 s. Later he sees us marking the position of x | = 0 m at time t | = 0 s. During those 0.29 s, he sees the point x | = 172 Mm move from x = 150 Mm to x = γx | = 1.15 × 172 Mm = 198 Mm. The observer in F | sees 198 Mm of x contracted into 172 Mm of x |, which is a contraction by a factor of γ. In general, distances in F are shrunk in the direction of v by a factor of γ when viewed from F |.
The Lorentz Contraction is what we call the shrinking of the length of moving objects in their direction of motion. We used large distances in our example above, but all lengths are contracted by γ. A 1-m ruler passing by at c/2 will appear to be only 0.67 m long. We don't usually observe rulers going by at the half the speed of light, but we do observe electrons going at 99% of the speed of light. The electron itself has no length, but it produces an electric field, and this field is compressed in the direction of motion by the Lorentz contraction. The voltage such an electron induces in a nearby wire is indeed exactly predicted by the contraction.
With v = c/2, consider an observer at x = 0 m in F. He watches the clocks on F |. At t = 1 s he sees the passing clock in F | reads γt = 1.15 s. Time appears to be passing more quickly on the moving frame of reference. A colleague in F at x = 150 Mm is also watching the clocks on F |, and at t = 1 s, he sees the clock at x | = 0 m pass by. That clock reads only 0.86 s. The apparant slowing of a moving clock is what we call time dilation. The clock at x = 0 m appears to be slow when viewed from F |. The clock at x | = 0 m appears to be slow when viewed from F.
The time dilation we just described is symmetric. But lest us break the symmetry by introducing acceleration. Our observer begins in F | at x | = 0 m moving at v = c/2. At t | = 1 s, she arrives at x = γc/2 = 172 Mm and observes that t = γ = 1.15 s. She stops moving at c/2 and enters F. Setting aside the damage that would occur to any person as a result of such a sudden change in velocity, she now finds herself at time 1.15 s in F. But in her counting of time only 1.0 s has passed since she began her journey. She now accelerates to velocity −c/2 and returns to point x = 0 m. Another 1.0 s passes for her, while another 1.15 s passes in F. She stops moving and returns to F. In total, 2.3 s have passed in F, but only 2.0 s for her.
If our observer left behind a twin at x = 0 m, we see that she is now younger than her twin. The twin paradox refers to the apparent violation of symmetry that occurs when one observer experiences a different passage of time from another, even though they end up in the same place. But we see that this is not a paradox at all, because there is one observer accelerates and the other does not. If a spaceship accelerates to c/2 and travels to the stars and back over twenty three Earth years, when it returns its crew will have aged by only twenty years. At 99% of the speed of light, γ = 7.1. If the ship is gone for 71 years, its crew will have aged only 10 years.
A quantity that remains unchanged as we move from any inertial frame F to any other inertial frame F | is Lorentz invariant. Suppose two events A and B are separated by a distance Δx and time Δt in F. Let Δs2 = c2Δt2 − Δx2. This quantity Δs2 turns out to be Lorentz invariant. It can be positive or negative, but it will be the same in any inertial frame for the same two events A and B. If Δs2 is positive, we say the proper time between A and B is s/c. The proper time between A and B is the time delay between A and B in an inertial frame in which the distance between them is zero. If Δs2 is negative, we say the proper distance between A and B is √(−Δs2)/c. The proper distance between A and B is the distance between them in an inertial frame in which the time delay between them is zero.
The forces generated by electric and magnetic fields, as well as by springs and collisions, are Lorentz invariant also, as we will see in Relativistic Collisions.
In the following exercises, you may assume c = 300 Mm/s.